Lineare Algebra

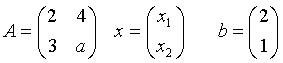
Hier geht es um Bereitstellung von Hilfsmitteln für die Beurteilung, ob ein lineares Gleichungssystem a) eindeutig b)mehrdeutig c) gar nicht lösbar ist und die Diagonalisierung von Matrizen oder auch die Bestimmung von Jordanschen Normalformen, wenn möglich.

Betrachten wir zunächst lineare Gleichungssysteme mit der Form Ax = b.

Hier ist A eine n*n-Matrix sowie x und b n-dimensionale Vektoren mit x als Lösungsvektor.
Ist das System eindeutig lösbar, so gilt für den Lösungsvektor x = A^-1b wobei A^-1 die Inverse der Koeffizientenmatrix A ist.
Zunächst sei die Frage gestellt, wann das System eindeutig lösbar ist. Dies ist genau dann der Fall, wenn die Determinante von A nicht 0 ist. 

Wir betrachten als Beispiel ein System für relle a wie folgt:

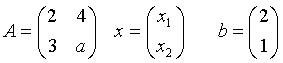
Zunächst untersuchen wir, für welche Werte von a das System gar nicht oder

mehrdeutig lösbar ist:

Es ist det A = 12 - 2a = 0, so dass nur a = 6 dafür in Frage kommt, dass das

System unlösbar oder mehrdeutig lösbar ist.

Nach elementaren Umformungen erkennt man für a = 6 die Unlösbarkeit, da

2 4 2

3 6 1

2 4 2

0 0 4

also 0 = 4. Dies ist eine falsche Aussage. In allen anderen Fällen liegt Eindeutigkeit vor.

Für die restlichen Werte von a gibt es ein eindeutiges Ergebnis, dass nachstehend hergeleitet wird:

Hierbei berechnen wir zunächst die Inverse von A und erhalten

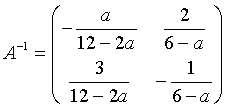
       Als Lösungsvektor ergibt sich x = A^-1b =                                                                                                    

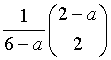
Weiterhin sieht man hieraus, dass für den Fall a=6 die Ränge der Koeffizientenmatrix A und der erweiterten Matrix (A,b) verschieden sind nämlich 1 = Rang A ¹ Rang (A;b) = 2.

Im Folgenden geht es nun um die Lösung eines linearen Gleichungssystems, das aus einer Gleichung und zwei Variablen besteht. Es wird eine mehrdeutige Lösung haben. Hier kann man nun eine Gesamtlösung entwickeln, die sich aus der Addition einer allgemeinen Lösung des homogenen Systems und einer speziellen Lösung des inhomogenen Systems zusammensetzt:

2x₁ + 3x₂ = 1

Zunächst ist zu sagen, dass wir uns hier noch eine zweite Zeile vorstellen müssen, deren Koeffizienten alle 0 sind. So ist hier Rang A = Rang (A,b) = 1 und somit das System lösbar. Weiter ist n - Rang A = 2 - 1 = 1 und somit eine Variable frei wählbar. n bezeichnet die Anzahl der Variblen.

Setze nun x₂ = l woraus sich x₁ = -3l/2 als allgemeine Lösung des homogenen Systems herauskristallisiert. Als eine spezielle Lösung des inhomogenen Systems erhält man x₁ = -1 und x₂ = 1

In Vektorenschreibweise sieht nun die Gesamtlösung des inhomogenen Systems wie folgt aus:

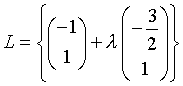
Diagonalisierung hermitescher und symmetrischer Matrizen

Zu jeder hermiteschen Matrix A = A^*existiert ebenfalls eine unitäre Matrix C mit C^*C=E so, dass C^*AC = D ist. Hierbei sind A,C und D und E als Einheitsmatrix n*n-Matrizen und D eine Diagonalmatrix in deren Hauptdiagonalen die Eigenwerte von A stehen und außerhalb nur Nullen.Es ist wichtig zu wissen, dass eine n*n-Matrix genau dann diagonalisierbar ist, wenn ihr charakteristisches Polynom vollständig in Linearfaktoren zerfällt. Dies ist das sogenannte Diagonalisierbarkeitskriterium.

Jede hermitesche Matrix besitzt ausschließlich reelle Eigenwerte

Beweis:

Sei A hermitesch. Dann gibt es eine unitäre Matrix C, so dass A = (CDC^*)= (CDC^*)^*= A^*= CD^*C^*
Daraus folgt D = D^* und somit l_i=l^*_i woraus sich die Behauptung für i = 1,...,n ergibt.

Man kann auf einfache Weise bei diesen Matrizen auch ihre Potenz berechnen:

Sei b eine beliebige natürliche Zahl, so gilt A^b = CDC^*CDC^*... (b-mal) so folgt A^b = CD^bC. Natürlich brauchen Matrizen nicht hermitesch oder symmetrisch zu sein, um diagonalisierbar zu sein. Einzig das Diagonalisierbarkeitskriterium ist hierfür ausschlaggebend. Ist A diagonalisierbar, so sagt man auch, dass A einer Diagonalmatrix ähnlich ist.

Als erstes Beispiel betrachte man eine Matrix 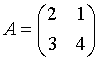, die selbst weder hermitesch noch symmetrisch ist, aber dennoch ähnlich zu einer Diagonalmatrix. Das charakteristische Polynom lautet det (A-lE)=(l-1)(l-5). Durch Gleichsetzen mit Null erhält man die beiden Eigenwerte l₁=1 und l₂=5.

Als Lösungsmenge des homogenen Gleichungssystems (A-lE)x = 0 mit x als Lösungs- und 0 als Nullvektor ergibt sich für beide Eigenwerte

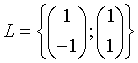
und als Lösung des Problems

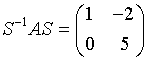
Die Eigenvektoren in den beiden Lösungsmengen L bilden eine Basis, da sie linear unabhängig sind. Dies kann man leicht daran erkennen, dass jeweils eine aus Ihnen zusammengesetzte Determinante ungleich 0 ist.

Allgemein definiert man die lineare Unabhängigkeit zweier Vektoren a und b so:

Zwei Vektoren a und b sind genau dann linear unabhängig, wenn es keine reelle Zahl x gibt, so dass a + x * b = 0 mit 0 als Nullvektor.

Sei A eine zur Diagonalmatrix D ähnliche Matrix. Dann gilt:

1. det A = det D

Beweis

det A = det (SDS^-1) = det S * det D * det S^-1= det (SS^-1) * det D = det D q.e.d

2. Spur A = Spur D

Beweis:

Spur A = Spur(SDS^-1)= Spur(D*SS^-1)= Spur D q.e.d

Wir sehen somit, dass die Spur einer diagonalisierbaren Matrix der Summe ihrer Eigenwerte entspricht.

Als nächstes betrachte man eine symmetrische Matrix A mit

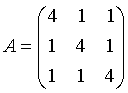
Das charakteristische Polynom lautet p(l)=(l-3)²(l-6) und somit erhält man den einfachen Eigenwert 6 und den zweifachen Eigenwert 3.

Im Folgenden bestimmt man nun die jeweilige Dimension der Lösungsräume zu beiden Eigenwerten. Wir erhalten für l=3

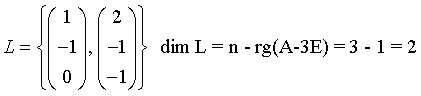
und für l=6

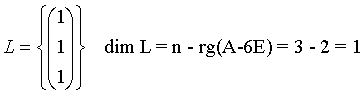
Somit ergeben sich die beiden folgenden Lösungsräume

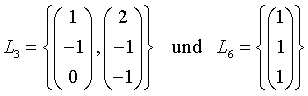
Man kann durch Bildung des Skalarprodukt beider Vektoren in L₃ erkennen,da dieses nicht 0 ist, dass diese beiden Vektoren nicht orthogonal zueinander sind. Aus diesem Grund findet hier das Schmidtsche Orthonormierungsverfahren wie folgt Anwendung

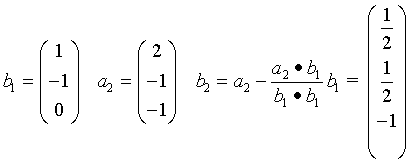
Wir erhalten

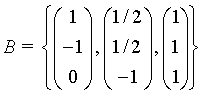
als Basis. Nach erfolgter Normierung der gerade berechneten Vektoren erhält man die gesuchte Matrix C mit

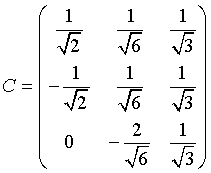
und man erhält

Hier ein allgemeingültiger Beweis zur Berechnung der Inversen einer hermiteschen Matrix A:

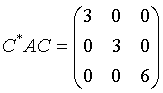
Beweis

Wie schon bekannt, gibt es eine Diagonalmatrix D und eine unitäre Matrix C mit CC^*=C^*C=E und A=CDC^*.

Hieraus folgt

A^-1=(CDC^*)^-1=(C^*)^-1D^-1C^-1=C*D^-1C^*

An dieser Stelle folgt die Betrachtung von Funktionen von Matrizen und als Beispiel hierfür die Funktion

f(A) = ln(E+A)

wobei A eine hermitesche n*n-Matrix sei und E die n*n-Einheitsmatrix.

Um fortzuführen, benutzen wir nun die aus dem Menüpunkt Analysis dieser Webseite gewonnene Taylorreihe und übertragen diese lediglich auf Matrizen. Dadurch, dass A hermitesch ist, existiert bekanntlich eine unitäre Matrix C mit A = CDC^* und man erhält insgesamt

ln(E+A) =S^¥_k=0(-1)^k-1(A^k/k) = CS^¥_k=0(-1)^k-1(D^k/k)C^*

Die Reihe ist zudem normkonvergent für

½½A½½₂ = ½½CDC^*½½₂ = ½½DCC^*½½₂ = ½½D½½₂ = (S_i=1ⁿl_i=1²)^1/2Î[0,1]

Hier zunächst ein allgemeiner Zusammenhang:

Sei l ein Eigenwert einer hermiteschen Matrix A sowie f eine mindestens (n+1)-mal differenzierbare und umkehrbare Funktion auf ihrem Definitionsintervall. Dann gilt:

1. f(A) ist hermitesch.

2. f(l) ist Eigenwert von f(A).

3. f(A) besitzt zu f(l) denselben Eigenvektor wie A zu l.

Beweis zu 1.:

Es sei A = A^* sowie f(A) = S^¥_k=0a_kA^k

Dann folgt hieraus

f(A) = f(A^*) = S^¥_k=0a_k(A^*)^k = S^¥_k=0a_k(A^k)^* = (S^¥_k=0a_kA^k)^* = f^*(A) q.e.d.

Beweis zu 2. und 3.

Nach der Eigenwertgleichung ergibt sich die Gleichung

Ax = lx

Hierbei ist x der zu l gehörende Eigenvektor.

Mit der Eigenschaft der Umkehrbarkeit von f ergibt sich zunächst

f ^-1f(A)x = f ^-1f(l)x

und somit

f(A)x = f(l)x q.e.d.

Dies bedeutet nichts anderes, dass für eine Funktion f mit obigen Eigenschaften und einer hermiteschen Matrix A = CDC^* folgt

f(A) = Cf(D)C^*

mit

f(D) = Diag(f(l₁),...,f(l_n))

Startseite

Empfehlung: Mathe-online